算法基础

算法基础

位运算解题

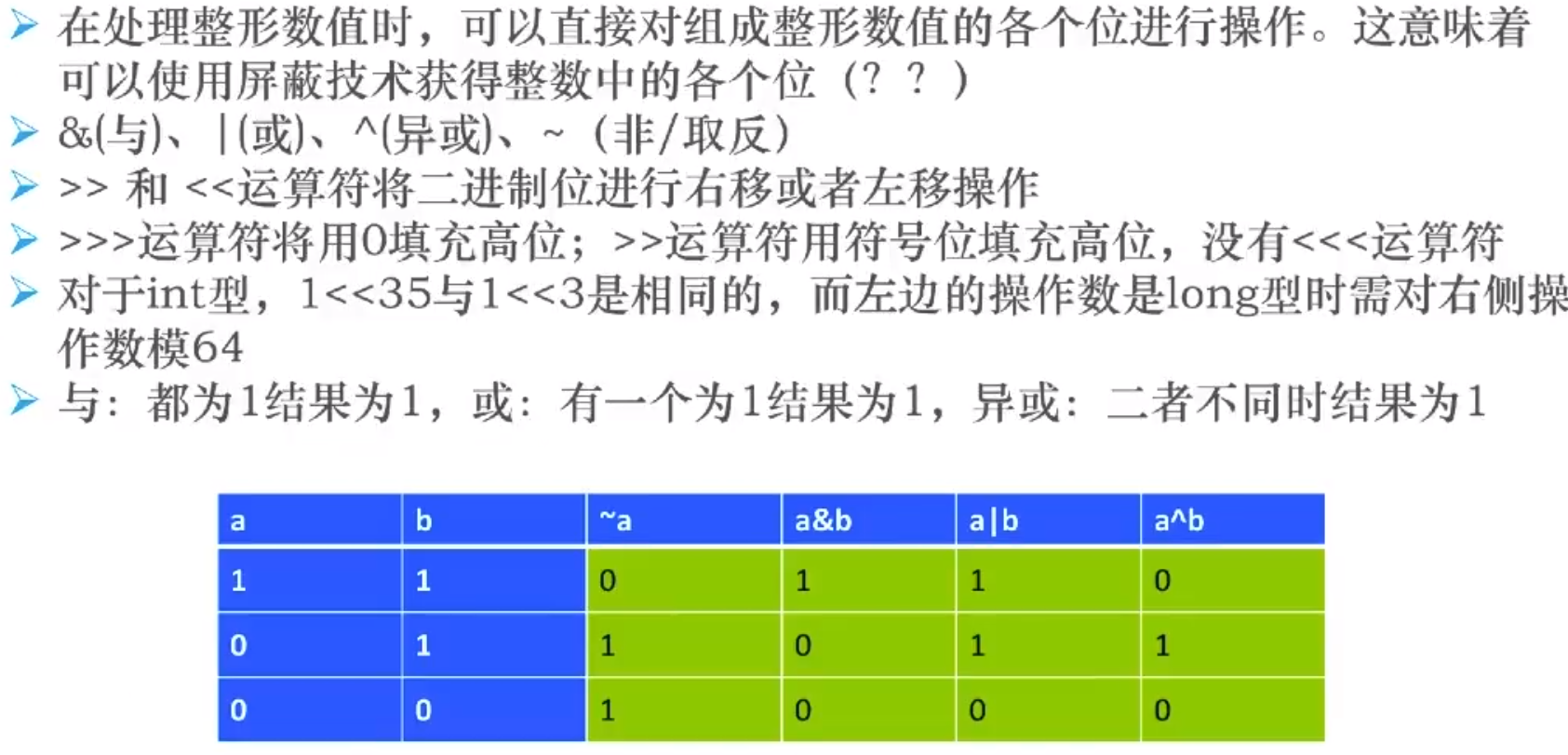
image-20221006100455290

image-20221006100423885

题1：找出数组中唯一成对的数

1-1000这1000个数放在含有1001个元素的数组中，只有唯一的一个元素值重复，其它均只出现一次。每个数组元素只能访问一次，设计一个算法，将它找出来;不用辅助存储空间，能否设计一个算法实现?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
package com.ep.bit;

import java.util.Random;

/***
 * @author dep
 * @version 1.0
 * 解题思路: 欧货相同为0,0和任何数异或都还得本身
 * a^b^c^a^b^c^d,利用交换律可以得到(a,a),(b,b),(c,c)异或为0,0和d异或就为d，这样就把d给找出来了
 + */
public class exercise1 {
    public static void main(String[] args) {
        int N = 1001;
        int[] arr = new int[N];
        for(int i = 0; i < arr.length - 1; i++) {
            arr[i] = i+1;
        }
        // 最后一个数，是随机数
        arr[arr.length -1] = new Random().nextInt(N-1) + 1;
        // 随机下标
        int index = new Random().nextInt(N);
        swap(arr,index, arr.length-1);
        print(arr);

        /**
         * 0异或任何数＝任何数
         * 1异或任何数－任何数取反
         * 任何数异或自己＝把自己置0
         * a^a=0；
         * a^0=a;
         * a^b=b^a，即交换律；
         */
        int x1 = 0;
        for (int i = 0; i <= N-1; i++) {
            x1 = (x1^i);
        }
        for (int i = 0; i < N; i++) {
            x1 = (x1^arr[i]);
        }
        System.out.println(x1);

        System.out.println("======================");
        // 方式二 暴力破解
        int helper[] = new int[N];
        for (int i = 0; i < N-1; i++) {
            helper[arr[i]]++;
        }
        for (int i = 0; i < N-1; i++) {
            if(helper[i] == 2) {
                System.out.println(i);
            }
        }

    }
    static void swap(int[] arr, int a, int b) {
        int t = arr[a];
        arr[a] = arr[b];
        arr[b] = t;
    }
    static void print(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            if(i == 0) {
                System.out.print("[");
            }
            System.out.print(arr[i]);
            if(i < arr.length-1) {
                System.out.print(",");
            }
        }
        System.out.println("]");
    }

}

题2: 找出落单的那个数

一个数组里除了某一个数字之外，其他的数字都出现了两次。请写程序找出这个只出现一次的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
package com.ep.bit;

/***
 * @author dep
 * @version 1.0
 * 一个数组里除了某一个数字之外，其他的数字都出现了两次。请写程序找出这个只出现一次的数字。
 */
public class exercise2 {
    public static void main(String[] args) {
        int[] arr = {1,1,2,2,3,3,4,5,4,5,0,0,10};
        int x1 = 0;
        for (int i = 0; i < arr.length; i++) {
            x1 = x1^arr[i];
        }
        System.out.println(x1);
    }
}

题3: 二进制中1的个数

请实现一个函数，输入一个整数，输出该数二进制表示中1的个数。

例:9的二进制表示为1001，有2位是1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
package com.ep.bit;

import java.util.Scanner;

/***
 * @author dep
 * @version 1.0
 * 请实现一个函数，输入一个整数，输出该数二进制表示中1的个数。
 * 例:9的二进制表示为1001，有2位是1
 */
public class exercise3 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int x = scanner.nextInt();
        // 方法一
        int s = 0;
        for (int i = 0; i < 32; i++) {
            if((x&(1<<i)) == (1<<i)) {
                s ++;
            }
        }
        System.out.println(s);


        // 方法二
        System.out.println("==============");
        int sum = 0;
        for (int i = 0; i < 32; i++) {
            if(((x>>i)&1) == 1) {
                sum ++;
            }
        }
        System.out.println(sum);

        System.out.println("==============");
        // 方法三
        int count = 0;
        while (x!=0) {
            x=((x-1)&x); // 消掉一个1
            count++;
        }
        System.out.println(count);
    }
}

题4: 是不是2的整数次方

用一条语句判断一个整数是不是2的整数次方。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
package com.ep.bit;

import java.util.Scanner;

/***
 * @author dep
 * @version 1.0
 * 用一条语句判断一个整数是不是2的整数次方。
 */
public class exercise4 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int num = scanner.nextInt();

        if(num !=0 && ((num-1)&num) == 0) {
            System.out.println(num + "是2的整数次方");
        }
    }
}

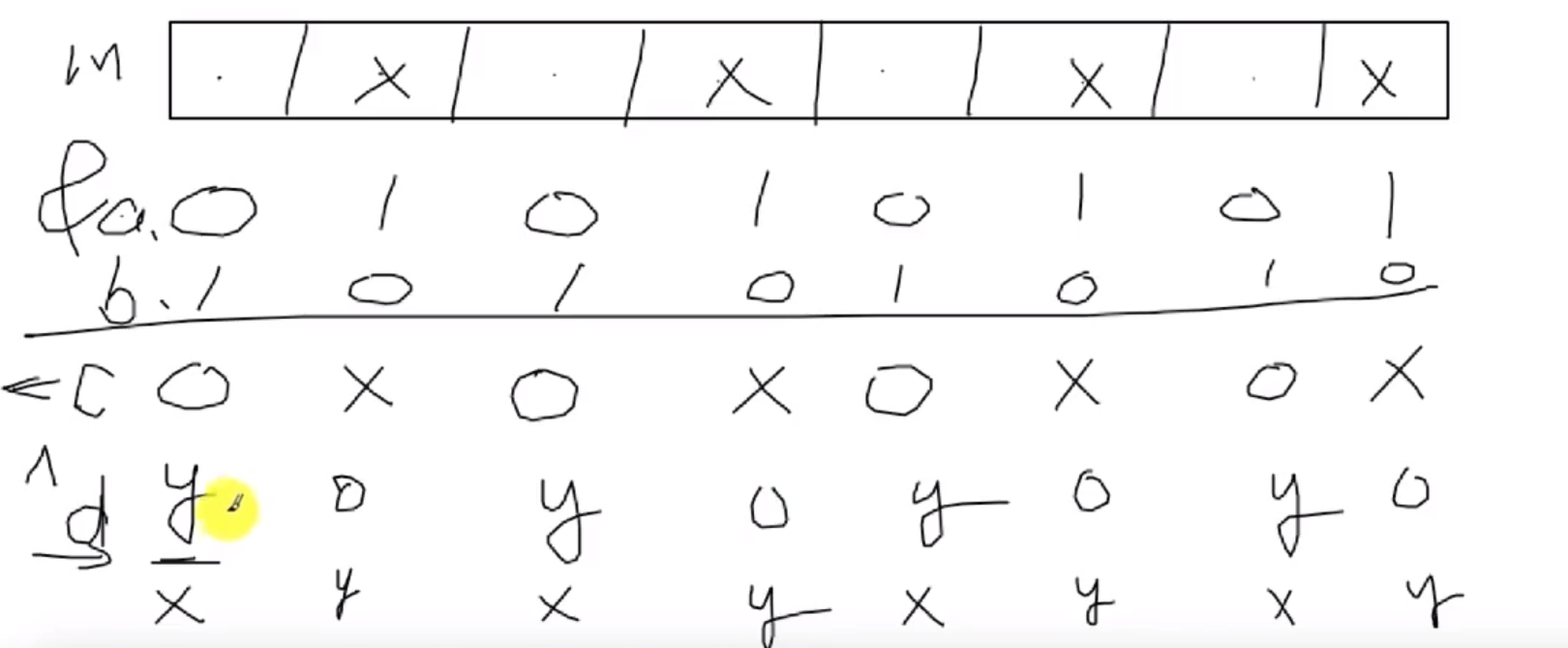
题5: 将整数的奇偶位互换

image-20221008132340425

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
package com.ep.bit;

import java.util.Scanner;

/***
 * @author dep
 * @version 1.0
 * 将整数的奇偶位互换
 */
public class exercise5 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int num = scanner.nextInt();
        System.out.println(swap(num));

    }
    public static int swap(int num) {
        int odd = num&0x55555555; // 和0101 0101 0101 0101 ...相与取出奇数位   // 原本的偶数位
        int even = num&0xaaaaaaaa; // 和1010 1010 1010 1010...相与取出偶数位    // 原本的奇数位
        return (odd<<1)^(even>>1); //连起来  (0与任何数异或得到的是本身)
    }
}

题6: 0~1间浮点实数的二进制表示

给定一个介于O和1之间的实数，(如0.625)，类型为double,打印它的二进制表示(0.101,
因为小数点后的二进制分别表示0.5,0.25.0.125……) 。
如果该数字无法精确地用32位以内的二进制表示，则打印“ERROR”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
package com.ep.bit;

import java.util.Scanner;

/***
 * @author dep
 * @version 1.0
 * 0~1间浮点实数的二进制表示
 */
public class exercise6 {
    /***
     * 给定一个介于O和1之间的实数，(如0.625)，类型为double,打印它的二进制表示(0.101,
     * 因为小数点后的二进制分别表示0.5,0.25.0.125......) 。
     * 如果该数字无法精确地用32位以内的二进制表示，则打印“ERROR”
     * @param args
     */
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        double num = scanner.nextDouble();
        StringBuilder stringBuilder = new StringBuilder("0.");
        while (num > 0) {
            // 乘以2
            double r = num*2;
            if(r >= 1) {
                stringBuilder.append("1");
                num = r-1;
            }else {
                stringBuilder.append("0");
                num  = r;
            }
            if(stringBuilder.length() > 34) {
                System.out.println("ERROR");
                return;
            }
        }
        System.out.println(stringBuilder.toString());

    }
}

题7: 出现k次与出现1次

数组中只有一个数出现了1次，其他的数都出现了k次，请输出只出现了1次的数。

K进制的数相加k次不进位加法结果是0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
package com.ep.bit;

/***
 * @author dep
 * @version 1.0
 * 数组中只有一个数出现了1次，其他的数都出现了k次，请输出只出现了1次的数。
 */
public class exercise7 {
    public static void main(String[] args) {
        int[] arr = {2,2,2,20,7,7,7,3,3,3,6,6,6,8,8,8};
        int len = arr.length;
        char [][] kRodix = new char[len][];
        int k = 3;
        int maxLen = 0;
        // 转成k进制字符串
        for(int i = 0; i < arr.length; i++){
            // 求每个数字的三进制字符串并翻转，然后转为字符数组
            kRodix[i] = new StringBuilder(Integer.toString(arr[i],k)).reverse().toString().toCharArray();
            if(kRodix[i].length > maxLen) {
                maxLen = kRodix[i].length;
            }
        }
        int[] resArr = new int[maxLen];
        for (int i = 0; i < len; i++) {
            // 不进位加法
            for (int j = 0; j < maxLen; j++) {
                if(j >= kRodix[i].length) {
                    resArr[j] += 0;
                } else {
                    resArr[j] += (kRodix[i][j] - '0');
                }
            }
        }
        int res = 0;
        for (int i = 0; i < maxLen; i++) {
             res += (resArr[i] % k) * (int)(Math.pow(k,i));
        }
        System.out.println(res);
    }
}

递归

求阶乘

打印i-j

数组求和

翻转字符串

斐波那契数

最大公约数

排序改递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
package com.ep.recursion;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 * 递归基础练习
 */
public class exercise1 {
    public static void main(String[] args) {
        System.out.println(f1(5));
        f2(1,9);
        int[] arr = {1,2,3,4,5};
        System.out.println(f3(arr, 0));

        String str = "abcd";
        System.out.println(reverse(str, str.length() - 1));

        System.out.println(f4(5));

        System.out.println(gcd(12,8));

        int[] arr2 = {1,5,6,9,8,7,5,3,6,9,10};
        insertSort(arr2, arr2.length-1);
        System.out.println(Arrays.toString(arr2));
    }

    /***
     * 递归求阶乘
     * @param n
     * @return
     */
    static int f1(int n) {
        if(n == 1)
            return 1;
        return n*f1(n-1);
    }

    /***
     * 递归打印i-j
     * @param i
     * @param j
     */
    static void f2(int i, int j) {
        if(i > j) {
            return;
        }
        System.out.println(i++);
        f2(i,j);
    }

    /**
     * 递归求数组之和
     * @param arr
     * @param start
     * @return
     */
    static int f3(int[] arr, int start) {
        if(start == arr.length -1 ) {
            return arr[start];
        }
        return arr[start] + f3(arr, start+1);
    }

    /***
     * 递归翻转字符串
     * 思路: 最后一个字母加其他几个翻转
     * @param
     */
    static String reverse(String src,  int end) {
        if(end == 0) {
            return "" + src.charAt(0);
        }
        return src.charAt(end) + reverse(src, end-1);
    }

    /***
     * 斐波那契数
     * @param n
     * @return
     */
    static int f4(int n) {
        if(n == 1 || n == 2) {
            return 1;
        }else {
            return f4(n-1) + f4(n-2);
        }
    }

    /***
     * 最大公约数
     * @param m
     * @param n
     * @return
     */
    static int gcd(int m, int n) {
        if (n == 0) {
            return m;
        }
        return gcd(n, m % n);
    }

    /***
     * 递归插入排序
     * @param arr
     * @param k
     */
    static void insertSort(int[] arr, int k) {
        if(k==0) {
            return;
        }
        // 对前k-1个元素排序
        insertSort(arr, k -1 );
        // 把位置为k的元素插入到前面部分
        int x = arr[k];
        int index = k - 1 ;
        while (index > -1 && x < arr[index]){
            arr[index+1] = arr[index]; // 后移一位
            index --;
        }
        arr[index+1] = x;
    }
}

递归技巧

找重复
1、我到一种划分方法
2，找到递推公式壹者等价转接都是父问题转化为求解子问题
找变化的量
变化的量遗常要作为参数

找出出口

汉诺塔

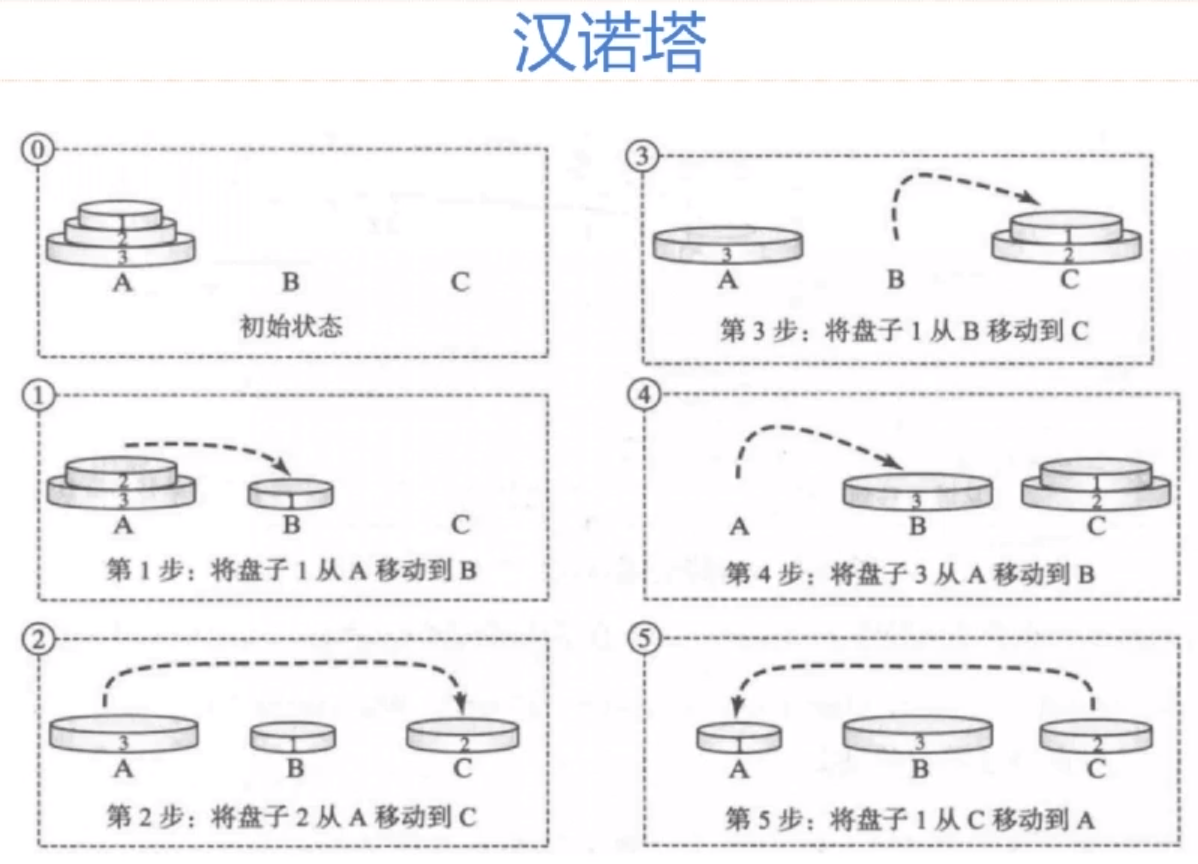
image-20221010095211656

1-N从A移动到B，C作为辅助

​ 等价于：

​ 1. 把1-n-1 从A移动到C，B作为辅助

  1. 把n从A移动到B

                           3. 1-n-1从c移动到B，A为辅助

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
package com.ep.recursion;

/***
 * @author dep
 * @version 1.0
 * 折半查找递归
 */
public class binSearch {
    public static void main(String[] args) {
        int[] arr = {1,5,6,8,9,12,15,16};
        System.out.println(binSearch(arr, 0, arr.length - 1, 5));
    }
    static int binSearch( int[] arr, int low, int high, int key) {
        if( low > high) {
            return -1;
        }
        int mid = low + ((high - low) >> 1); // 右移一位相当于除以2
        int midVal = arr[mid];
        if(midVal < key) {
            return binSearch(arr, mid+1, high, key);
        } else if(midVal > key) {
            return binSearch(arr, low, mid-1,key);
        } else
            return mid;
    }
}

折半查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
package com.ep.recursion;

/***
 * @author dep
 * @version 1.0
 * 折半查找递归
 */
public class binSearch {
    public static void main(String[] args) {
        int[] arr = {1,5,6,8,9,12,15,16};
        System.out.println(binSearch(arr, 0, arr.length - 1, 5));
    }
    static int binSearch( int[] arr, int low, int high, int key) {
        if( low > high) {
            return -1;
        }
        int mid = low + ((high - low) >> 1); // 右移一位相当于除以2
        int midVal = arr[mid];
        if(midVal < key) {
            return binSearch(arr, mid+1, high, key);
        } else if(midVal > key) {
            return binSearch(arr, low, mid-1,key);
        } else
            return mid;
    }
}

希尔排序（未用递归）

希尔排序也是一种插入排序，它是简单插入排序经过改进之后的个更高效的版本，也称为缩小增量排序

希尔排序是插入排序的一种。
也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法
思路:如序列9 8 7 6 5 4 3 2 1

数值 9 8 7 6 5 4 3 2 1
下标 0 1 2 3 4 5 6 7 8

​ 确定-增量序列，如4(length/2)2 1，从大到小使用增量
​ 使用第一个增量4，将序列划分为若干个子序列，下标组合为0-4-8，1-5,2-6,3-7
​ 依次对子序列使用直接插入排序法;
​ 使用第二个增量2，将序列划分为若干个子序列(0-2-4-6-8),(1-3-5-7)
​ 依次对子序列使用直接插入排序法:
​ 使用第三个增量1，这时子序列就是元序列（0-1-2-3-4-5-6-7-8)，使用直接插入完成排序。

时间复杂度:不太确定在0 (nlogn)~0 (n2)之间

空间复杂度:0(1)
原址排序
稳定性:由于相同的元素可能会被划分至不同子序列单独排序，因此稳定性是无法保证的–不稳定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
package com.ep.recursion;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 * 希尔排序
 */
public class shellSort {
    public static void main(String[] args) {
        int[] arr = {9,8,7,6,5,4,3,2,1};
        shellSort(arr);
        System.out.println(Arrays.toString(arr));

    }
    static void shellSort(int[] arr) {
        for (int interval = arr.length /2; interval >= 1 ; interval = interval / 2 ) {
            // 在增量为interval的插入排序
            for (int i = interval; i < arr.length; i++) {
                int target = arr[i];
                int j = i - interval;
                while (j > -1 && target < arr[j]) {
                    arr[j+ interval] = arr[j];
                    j-=interval;
                }
                arr[j+interval] = target;
            }
        }
    }
}

题1:小白上楼梯（递归设计)

小白正在上楼梯，楼梯有n阶台阶，小白一次可以上1阶，2阶或者3阶，实现一个方法，计算小白有多少种
走完楼梯的方式。

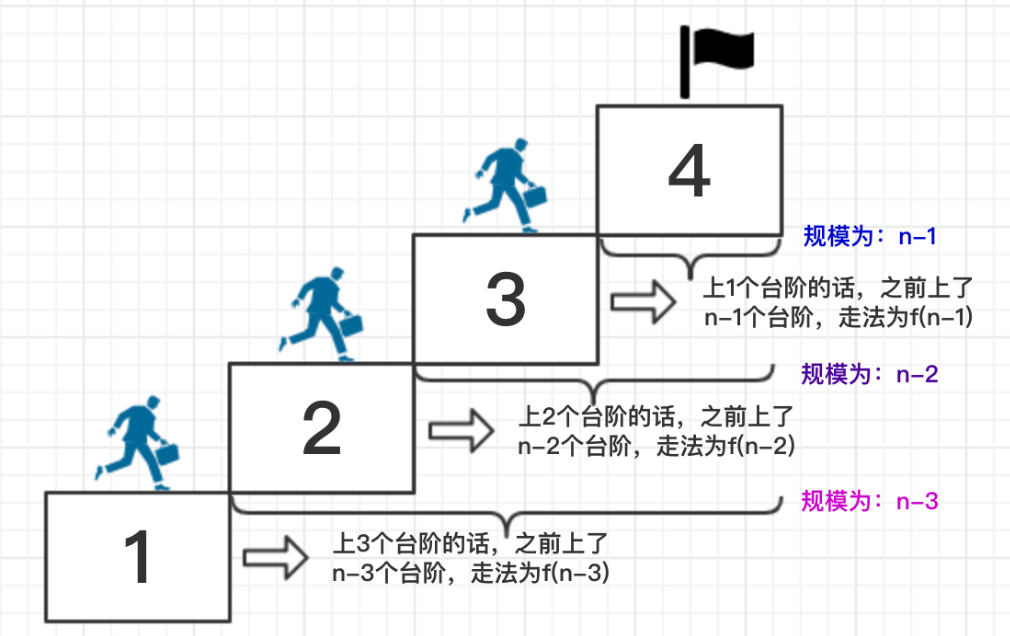
image-20221011140647413

运用逆推原理

当有n个台阶（n>3）时，可以这样想：

  • 最后是一步上1个台阶的话，之前上了n-1个台阶，走法为f(n-1)种，
  • 而最后是一步上2个台阶的话，之前上了n-2个台阶，走法为f(n-2)种，
  • 而最后是一步上3个台阶的话，之前上了n-3个台阶，走法为f(n-3)种故而f(n)=f(n-1)+f(n-2)+f(n-3)。
  • 列出的递归方程为：f(1)=1;f(2)=2;f(3)=4;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
package com.ep.recursion;

import java.util.Scanner;

/***
 * @author dep
 * @version 1.0
 * 小白上楼梯（递归设计)
 * 小白正在上楼梯，楼梯有n阶台阶，小白一次可以上1阶，2阶或者3阶，实现一个方法，计算小白有多少种
 * 走完楼梯的方式。
 */
public class exercise3 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (true) {
            int n = scanner.nextInt();
            System.out.println(f(n));
        }
    }
    static int f(int n) {
        if(n == 0) return 1;
        if(n == 1) return 1;
        if(n == 2) return 2;
        return f(n-1) + f(n-2) + f(n-3);
    }
}

时间复杂度

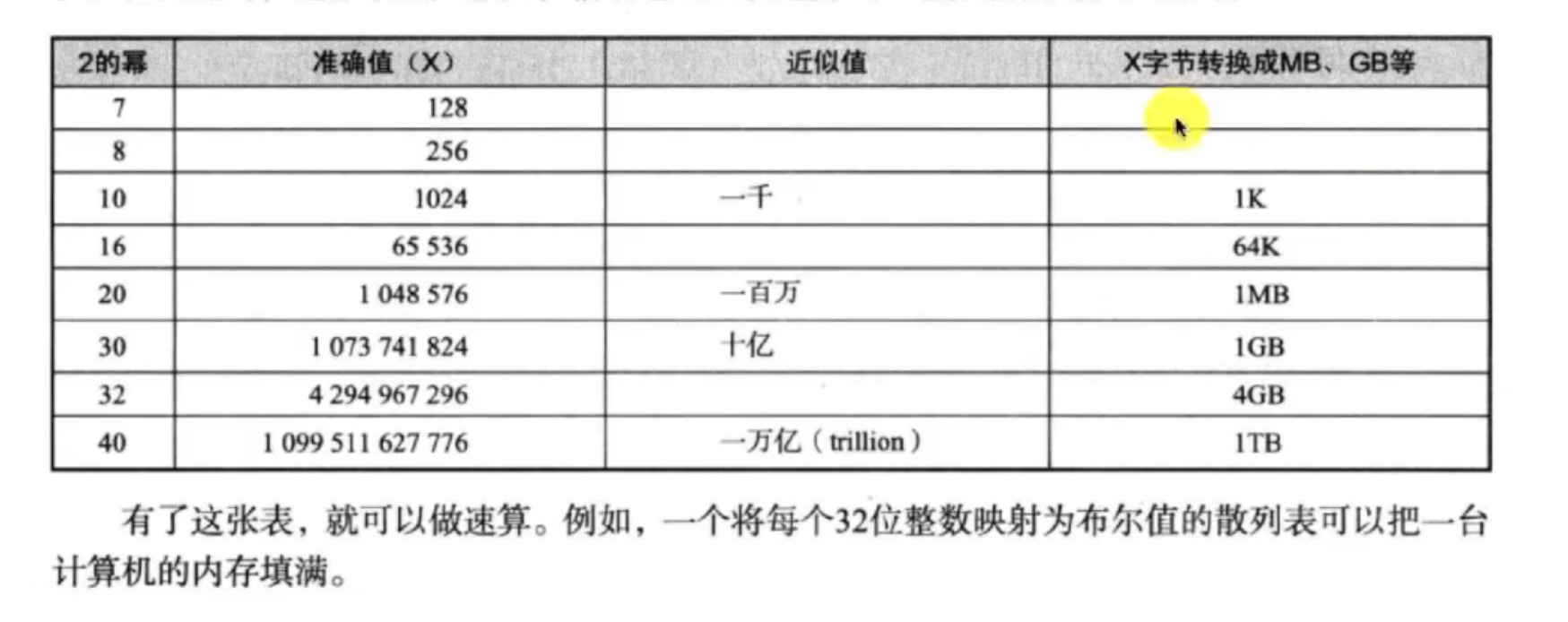
image-20221011110509645

练习

题2∶旋转数组的最小数字（改造二分法)

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的-个旋转，该数组的最小值为1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
package com.ep.recursion;

/***
 * @author dep
 * @version 1.0
 * 旋转数组的最小数字（改造二分法)
 * 把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。
 * 例如数组{3,4,5,1,2}为{1,2,3,4,5}的-个旋转，该数组的最小值为1.
 */
public class exercise4 {
    public static void main(String[] args) {
        int arr[] = {3,4,5,1,2};
        System.out.println(min(arr));

        int arr1[] = {1,0,1,1,1};
        System.out.println(min(arr1));
    }
    static int min(int[] arr) {
        int begin = 0;
        int end = arr.length - 1;
        // 考虑没有旋转这这种特殊的旋转
        if(arr[begin] < arr[end]) return arr[begin];
        if(arr[begin] == arr[end]) {
            System.out.println("应该用顺序查找");
            return -1;
        }
        // begin和end指向相邻元素，退出
        while(begin + 1 < end) {
            int mid = begin + ((end-begin) >> 1);
            // 要么左侧有序，要么右侧有序
            if(arr[mid] >= arr[begin]) { // 左侧有序
                begin = mid;
            }else {
                end = mid;
            }
        }
        return arr[end];
    }
}

题3∶在有空字符串的有序字符串数组中查找

有个排序后的字符串数组，其中散布着一些空字符串，编写一个方法，找出给定字符串（肯定不是空字符串）的索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
package com.ep.recursion;

/***
 * @author dep
 * @version 1.0
 * 在有空字符串的有序字符串数组中查找
 * 有个排序后的字符串数组，其中散布着一些空字符串，编写一个方法，找出给定字符串（肯定不是空字符串）的索引。
 */
public class exercise5 {
    public static void main(String[] args) {
        String[] strs = {"a","","ab","b","","cc","cd","dd"};
        String p = "cc";
        System.out.println(indexOf(strs, p));
    }
    static int indexOf(String[] arr, String p) {
        int begin = 0;
        int end = arr.length - 1;
        while(begin <= end) {
            int indexOfMid = begin + ((end - begin) >> 1);
            while(arr[indexOfMid].equals("")) {
                indexOfMid ++;
            }
            if(arr[indexOfMid].compareTo(p) > 0) {
                end = indexOfMid - 1;
            }else if(arr[indexOfMid].compareTo(p) < 0) {
                begin = indexOfMid + 1;
            } else {
                return indexOfMid;
            }
        }
        return -1;
    }
}

题4∶最长连续递增子序列（部分有序）

(1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
package com.ep.example;

import java.sql.Array;
import java.util.Arrays;
/***
 * @author dep
 * @version 1.0
 * 最长连续递增子序列（部分有序）
 * (1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)。
 */
public class exercise3 {
    public static void main(String[] args) {
        int arr[] = {1,9,2,5,7,3,4,6,8,0};
        int res[] = new int[arr.length];
        int max = 0;
        for (int i = 0; i < arr.length - 1; i++) {
          if(arr[i] < arr[i+1]) {
            max ++ ;
          } else {
              res[i] = max;
              max = 0;
          }
          if(i + 1 == arr.length - 1) {
              res[i+1] = max;
          }
        }
//        System.out.println(Arrays.toString(res));
        int maxVal = 0;
        int indexOf = 0;
        for (int i = 0; i < res.length; i++) {
            if(res[i] >= maxVal) {
                maxVal = res[i];
                indexOf = i;
            }
        }
        int result[] = new  int[maxVal + 1];
        System.arraycopy(arr,indexOf - maxVal, result, 0, maxVal + 1);
        System.out.println(Arrays.toString(result));
    }
}

题5:设计一个高效的求a的n次幂的算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
package com.ep.example;

/***
 * @author dep
 * @version 1.0
 * 题5:设计一个高效的求a的n次幂的算法
 */
public class exercise4 {
    public static void main(String[] args) {
        long t = System.nanoTime();
        System.out.println(pow0(2,30));
        System.out.println("时间：" + (System.nanoTime() - t));
        t = System.nanoTime();
        System.out.println(pow(2,30));
        System.out.println("时间：" + (System.nanoTime() - t));
    }
    static int pow0(int a, int n) {
        int res = 1;
        for (int i = 0; i < n; i++) {
            res*=a;
        }
        return res;
    }
    static int pow(int a, int n) {
        if(n == 0) return 1;
        int res = a;
        int ex = 1;
        // 左移1位，相当于乘以2
        while ((ex<<1) <=n ){
            res = res*res;
            ex <<= 1;
        }
        // 查差n-ex的次方没有去乘到结果里面
        return res*pow(a, n-ex);
    }
}

查找与排序

分治法

分治法(divide and conquer, D&C)∶将原问题划分成若干个规模较小而结构与原问题一致的子问题﹔递归地解决这些子问题，然后再合并其结果，就得到原问题的解。
容易确定运行时间，是分治算法的优点之一。

分治模式在每一层递归上都有三个步骤

  • 分解(Divide):将原问题分解成一系列子问题;
  • 解决(Conquer):递归地解各子问题。若子问题足够小,则直接有解;
  • 合并(combine):将子问题的结果合并成原问题的解。

快速排序算法

快速排序算法
1、分解∶数组A[p.r]被划分为两个子数组A[p..q-1]和A [ q+1,r]，使得A[ q]为大小居中的数，左侧A[p..q-1]中的每个元素都小于等于它,而右侧A [ q+1,r]中的每个元秦都大于等于它。
其中计算下标q也是划分过
程的一部分。
2、解决︰通过递归调用快速排序，对子数组A[p..q-1]和A[ q+1,r]进行排序

3、合并:因为子数组都是原址排序的，所以不需要合并，数组A[p..r]
已经有序

那么，划分就是问题的关键+

快速排序之单向扫描法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
package com.ep.example;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 * 快速排序单项扫描法
 */
public class exercise5 {
    public static void main(String[] args) {
        int[] arr = {5,1,6,8,9,10,2,3,11};
        quickSort(arr,0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    public static void quickSort(int[] A, int p, int r) {
        if(p < r) {
            int q = partition(A,p,r);
            quickSort(A,p,q-1); // 左侧快速排序
            quickSort(A,q+1,r); // 右侧快速排序
        }
    }
    public static int partition(int[] arr, int p, int r) {
        int pivot = arr[p];
        int scanner = p + 1; // 扫描指针
        int right = r; // 右侧指针
        while(scanner <= right) {
            if(arr[scanner] < pivot) {
                scanner ++ ;
            }else {
                // 找到左侧大的和右侧进行交换
                swap(arr, scanner, right);
                right--;
            }
        }
        swap(arr, p, right);
        return right;
    }

    /***
     * 交换数组的值
     * @param arr
     * @param m
     * @param n
     */
    static void swap (int[] arr, int m , int n) {
        int num = arr[m];
        arr[m] = arr[n];
        arr[n] = num;
    }
}

双向扫描法

双向扫描的思路是，头尾指针往中间扫描，从左找到大于主元的元素，从右找到小于等于主元的元素二者交换，继续扫描，直到左侧无大元素，右侧无小元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
package com.ep.example;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 * 快速排序双向扫描
 */
public class exercise6 {
    public static void main(String[] args) {
        int[] arr = {5,1,6,8,9,10,2,3,11};
        quickSort(arr,0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    public static void quickSort(int[] A, int p, int r) {
        if(p < r) {
            int q = partition2(A,p,r);
            quickSort(A,p,q-1); // 左侧快速排序
            quickSort(A,q+1,r); // 右侧快速排序
        }
    }
    public static int partition2(int[] arr, int p, int r) {
        int pivot = arr[p];
        int left = p + 1; // 扫描指针
        int right = r; // 右侧指针
        while(left <= right) {
           // left不停往右走，直到遇到大于主元的元素
            if(left <= right && arr[left] <= pivot) left++; // 循环退出时，left一定是指向第一个大于主元的位置
            if(left <= right && arr[right] > pivot) right--; // 循环退出时，right一定是指向最后一个小于等于主元素的
            if(left < right) {
                swap(arr, left, right);
            }
        }
        // while退出时，两者交错，且right指向的最后一个小于等于主元的位置，也就是主元应该呆的位置
        swap(arr, p, right);
        return right;
    }
    /***
     * 交换数组的值
     * @param arr
     * @param m
     * @param n
     */
    static void swap (int[] arr, int m , int n) {
        int num = arr[m];
        arr[m] = arr[n];
        arr[n] = num;
    }
}

有相同元素值的快速排序——三分法

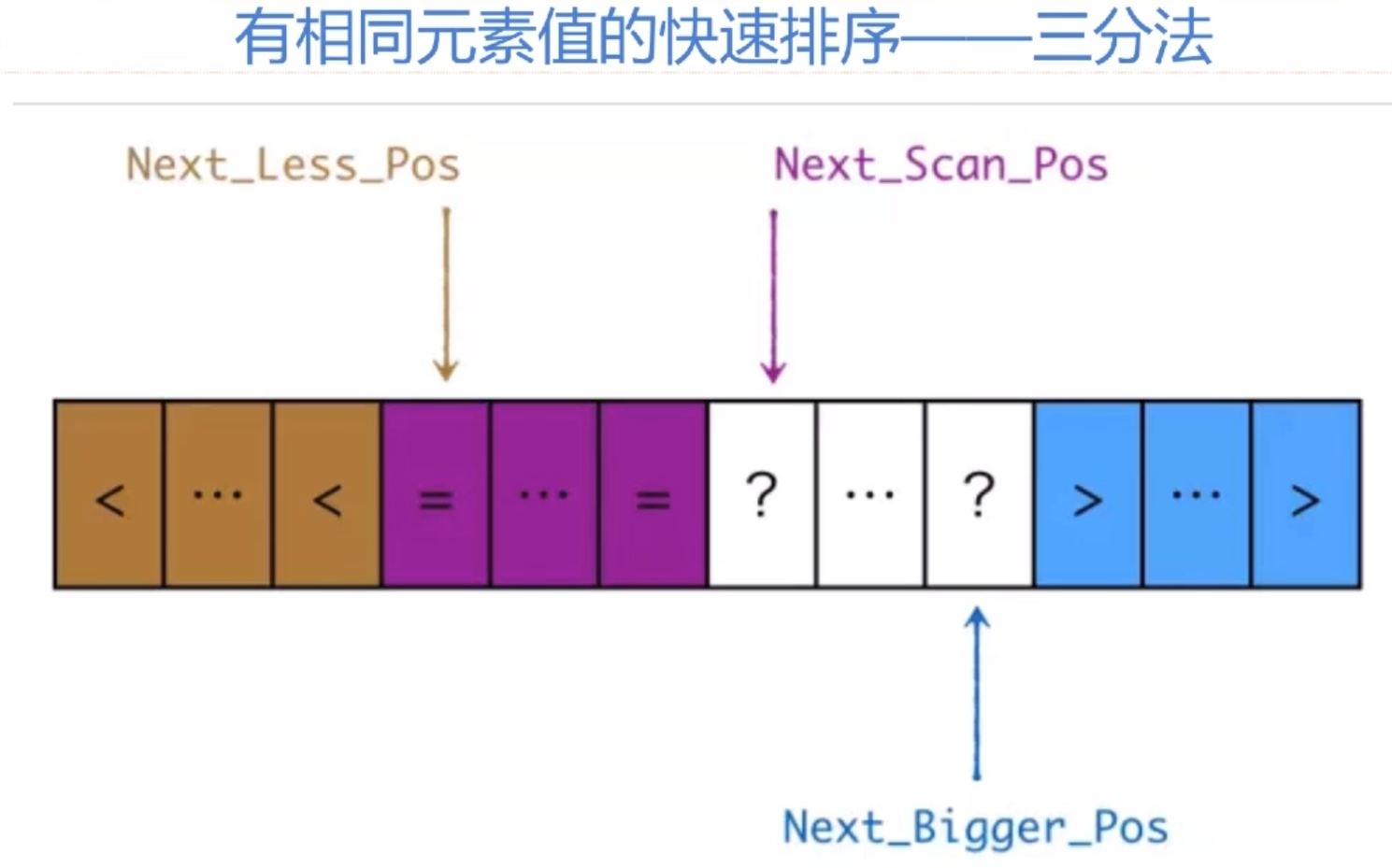
image-20221013100611514

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
package com.ep.example;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 */
public class exercise7 {
    public static void main(String[] args) {
        int[] arr = {5,1,6,8,9,10,2,3,11};
        quickSort(arr,0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    public static void quickSort(int[] A, int p, int r) {
        if(p < r) {
            int q = partition2(A,p,r);
            quickSort(A,p,q-1); // 左侧快速排序
            quickSort(A,q+1,r); // 右侧快速排序
        }
    }
    public static int partition2(int[] arr, int p, int r) {
        // 优化，在p,r,mid之间，选一个中间值作为主元
        int midIndex = p + (((r-p))>>1); // 中间下标
        int midValueIndex = -1; // 中值的下标
        if(arr[p] <= arr[midIndex] && arr[p] >= arr[r]) {
            midValueIndex = p;
        }else if(arr[r] <= arr[midIndex] && arr[r] >= arr[p]) {
            midValueIndex = r;
        } else {
            midValueIndex = midIndex;
        }
        swap(arr, p, midValueIndex);
        int pivot = arr[p];
        int left = p + 1; // 扫描指针
        int right = r; // 右侧指针
        while(left <= right) {
            // left不停往右走，直到遇到大于主元的元素
            if(left <= right && arr[left] <= pivot) left++; // 循环退出时，left一定是指向第一个大于主元的位置
            if(left <= right && arr[right] > pivot) right--; // 循环退出时，right一定是指向最后一个小于等于主元素的
            if(left < right) {
                swap(arr, left, right);
            }
        }
        // while退出时，两者交错，且right指向的最后一个小于等于主元的位置，也就是主元应该呆的位置
        swap(arr, p, right);
        return right;
    }
    /***
     * 交换数组的值
     * @param arr
     * @param m
     * @param n
     */
    static void swap (int[] arr, int m , int n) {
        int num = arr[m];
        arr[m] = arr[n];
        arr[n] = num;
    }
}

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
package com.ep.example;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 * 归并排序
 */
public class exercise8 {
    static int[] helper;
    public static void main(String[] args) {
        int[] arr= {1,5,3,6,9,8,7,4,1};
        helper = new int[arr.length];
        mergeSort(arr,0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    static void  mergeSort(int[] arr, int p, int r) {
        if( p < r ) {
           int mid = p + ((r-p) >> 1);
           mergeSort(arr,p, mid); // 左侧排序
           mergeSort(arr,mid+1, r); // 右侧排序
            merge(arr,p,mid,r); // 合并
        }
    }
    static void merge(int[] arr,int p, int mid, int r) {
        // 先把arr中的数据拷贝到helper中
        System.arraycopy(arr, p ,helper, p, r-p+1);
        int left = p; // 左侧队伍的头部指针，指向待比较的元素
        int right = mid + 1; // 右侧队伍的头部指针，指向待比较的元素
        int current = p; // 原数组的指针，指向带填入数据的位置

        while(left <= mid && right <= r) {
            if(helper[left] <= helper[right]) {
                arr[current] = helper[right];
                current++;
                left++;
            }else {
                arr[current] = helper[right];
                current++;
                right++;
            }
        }
        while(left <= mid) {
            arr[current] = helper[left];
            current++;
            left++;
        }
        while(right <= r) {
            arr[current] = helper[right];
            current++;
            right++;
        }
    }
}

算法案例

调整数组顺序使奇数位于偶数前面

调整数组顺序使奇数位于偶数前面:输入一个整数数组，调整数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。要求时间复杂度为O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
package com.ep.example;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 * 调整数组顺序使奇数位于偶数前面
 */
public class exercise9 {
    public static void main(String[] args) {
        int[] arr= {1,3,6,2,4,5,8,9,7,4,5,3};
        f(arr,0, arr.length - 1);
        System.out.println(Arrays.toString(arr));

    }
    static void f(int[] arr, int p, int r) {
        int left = p;
        int right = r;
        while(left < right) {
            if (!isEven(arr[left])) {  // 奇数
                left++;
                continue;
            }
           if (isEven(arr[right])) { // 偶数
               right--;
               continue;
           }
           swap(arr, left, right);
           left++;
           right--;
        }
    }

    /***
     * 交换
     * @param arr
     * @param p
     * @param r
     */
    static void swap(int arr[], int p, int r) {
        int t = arr[p];
        arr[p] = arr[r];
        arr[r] = t;
    }

    /***
     * 判断是否是偶数
     * @param p
     * @return
     */
    static Boolean isEven(int p) {
        return (p&1) == 0;
    }
}

第k个元素

第k个元素∶以尽量高的效率求出一个乱序数组中按数值顺序的第K个元素值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
package com.ep.example;

/***
 * @author dep
 * @version 1.0
 * 以尽量高的效率求出一个乱序数组中按数值顺序的第K个元素值
 */
public class exercise10 {
    public static void main(String[] args) {
        int[] arr = {1,3,6,5,8,9,4,2,5,7};
        System.out.println(selectK(arr, 0, arr.length - 1, 1));
        System.out.println(selectK(arr, 0, arr.length - 1, 3));
        System.out.println(selectK(arr, 0, arr.length - 1, 5));
        System.out.println(selectK(arr, 0, arr.length - 1, 7));
        System.out.println(selectK(arr, 0, arr.length - 1, arr.length));
    }

    /***
     * 查找第k个元素
     * @param arr
     * @param p
     * @param r
     * @param k
     * @return
     */
    static int selectK(int[] arr, int p, int r, int k) {
        int q = partition(arr,p,r);
        int qk = q-p+1; // 主元是第几个元素
        if( qk == k) {
            return arr[q];
        }else if( qk > k) {
            return selectK(arr, p, q-1, k);
        } else {
            // 右侧查找的应该是第k-qk个
            return selectK(arr, q+1, r, k - qk);
        }
    }
    /**
     * 确定中间的元素的位置
     * @param arr
     * @param p
     * @param r
     * @return
     */
    static int partition(int[] arr, int p, int r) {
        int pivot = arr[p];
        int left = p + 1;
        int right = r;
        while( left <= right ) {
            if(left <= right && arr[left] <= pivot) left++;
            if(left <= right && arr[right] > pivot) right--;
            if(left < right) {
                swap(arr, left, right);
            }
        }
        swap(arr,p,right);
        return right;
    }

    /***
     * 交换元素
     * @param arr
     * @param m
     * @param n
     */
    static void swap(int[] arr, int m, int n) {
        int t = arr[m];
        arr[m] = arr[n];
        arr[n] = t;
    }
}

超过一半的数字

超过一半的数字︰数组中有一个数字出现的次数超过了数组长度的一半，找出这个数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
package com.ep.example;

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
import java.util.Set;

/***
 * @author dep
 * @version 1.0
 * 超过一半的数字
 * //数组中出现次数超过半数的元素
 * 解法1:排序后返回arr[N/2]
 * 解法2: hash统计
 * 解法3:顺统计
 * 解法4:不同的数，进行消除
 */
public class exercise11 {
    public static void main(String[] args) {
        int []arr= {1,5,2,3,2,2,2};
        System.out.println(f(arr));
        System.out.println(f2(arr));
        System.out.println(f3(arr));
        System.out.println(f4(arr));
    }
    // 解法1:排序后返回arr[N/2]
    static int f(int[] arr) {
        Arrays.sort(arr);
        return arr[arr.length/2];
    }
    // 解法2: hash统计
    static int f2(int[] arr) {
        HashMap<Integer, Integer> hashMap = new HashMap();
        for (int i = 0; i < arr.length; i++) {
            if (hashMap.containsKey(arr[i])) {
                Integer count = hashMap.get(arr[i]);
                count++;
                hashMap.put(arr[i],count);
            }else {
                hashMap.put(arr[i],1);
            }
        }
        Set entrySet = hashMap.entrySet();
        for (Object entry: entrySet) {
            Map.Entry mapEntry = (Map.Entry) entry;
            if ((Integer)mapEntry.getValue() > arr.length / 2) {
                return (Integer) mapEntry.getKey();
            }
        }
        return -1;
    }
    // 解法3：顺序统计
    static int f3(int[] arr) {
        return exercise10.selectK(arr,0,arr.length-1,arr.length/2);
    }
    // 解法4：不同的数，进行消除(原理，相邻两个元素，如果不同就消除)
    static int f4(int[] arr) {
        // 候选数
        int candidate = arr[0];
        // 出现的次数
        int nTimes = 1;
        // 扫描数组
        for (int i = 1; i < arr.length; i++) {
            // 两两消减为0，应该把现在的元素作为候选值
            if (nTimes == 0) {
                candidate = arr[i];
                nTimes = 1;
                continue;
            }
            // 遇到和候选值相同的，次数都加1
            if(arr[i] == candidate) {
                nTimes++;
            }else {
                // 不同的数，进行消减
                nTimes--;
            }
        }
        return candidate;
    }
}

扩展：寻找发帖“水王”

Tango是微软亚洲研究院的一个试验项目。研究院的员工和实习生们都很喜欢在·Tango 上面交流灌水。传说，Tango有一大“水王”，他不但喜欢发贴，还会回复其他ID发的每个帖子。坊间风闻该“水王”发帖数目超过了帖子总数的一半。如果你有一个当前论坛上所有帖子（包括回帖）的列表，其中帖子作者的ID也在表中，你能快速找出这个传说中的Tango水王吗?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
     * //变化，出现次数恰好为个数的一半，求出这个数
     * 关于加强版水王的题我有个想法可以扫描一遍数组就解决问题：
     * 水王占总数的一半，说明总数必为偶数；
     * 不失一般性，假设隔一个数就是水王的id，两两不同最后一定会消减为0
     * 水王可能是最后一个元素，每次扫描的时候，多一个动作，和最后一个元素做比较，单独计数，计数恰好等于一半
     * 如果不是，计数不足一半，那么去掉最后一个元素，水王就是留下的那个candidate
     * */
    static int f5(int arr[]) {
        // 候选数
        int candidate = arr[0];
        int nTimes = 0;
        int countOfLast = 0; // 统计最后这个元素出现的次数
        int N = arr.length;

        for (int i = 0; i < N; i++) {
            // 增加和最后一个元素比较的步骤
            if(arr[i] == arr[N-1]) countOfLast++;
            if(nTimes == 0) {
                candidate = arr[i];
                nTimes++;
                continue;
            }
            if(arr[i] == candidate) {
                nTimes++;
            }else {
                nTimes--;
            }
        }
        // 最后一个元素出现的次数是n/2
        if(countOfLast == N/2 ){
           return arr[N-1];
        }else {
           return candidate;
        }
    }

最小可用ID

最小可用ID∶在非负数组（乱序)中找到最小的可分配的id (从1开始编号)，数据量1000000

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
package com.ep.example;


import org.lanqiao.algo.util.Util;

import java.util.Arrays;

/***
 * @author dep
 * @version 1.0
 * 解决最小可用id问题： 在非负数组（乱序）中找到最小的可分配的id（从1开始编号）
 */
public class exercise12 {

    //  O(N²) 暴力解法:从1开始依次探测每个自然数是否在数组中
    static int find1(int[] arr) {
        int i = 1;
        while(true) {
            // 逐个进行查找
            if(Util.indexOf(arr, i) == -1) {
                return i;
            }
            i++;
        }
    }

    static int find2(int[] arr) {
        Arrays.sort(arr); // NlogN
        int i = 0;
        while (i< arr.length) {
            if (i+1 != arr[i]) { // //不在位的最小的自然数
                return i+1;
            }
            i++;
        }
        return i+1;
    }

    /**
     * 改进1：改用辅助数组
     * @param arr
     * @return
     */
   static int find3(int[] arr) {
        int N = arr.length;
        int[] helper = new int[N + 1];
       for (int i = 0; i < N; i++) {
           if ( arr[i] < N+1) {
               helper[arr[i]] = 1;
           }
       }
       for (int i = 1; i <=N ; i++) {
           if(helper[i] == 0) {
               return i;
           }
       }
       return N+1;
   }

   static int find4(int[] arr, int l ,int r) {
       if(l > r) {
           return l + 1;
       }
       int midIndex = l + ((r-l) >> 2); // 中间坐标
       int q = exercise10.selectK(arr, l, r, midIndex -l +1); // 实际在中间位置的值
       int t = midIndex + 1; // 期望值
       if( q== t ){ // 左侧紧密 （说明在右侧）
           return find4(arr, midIndex + 1, r);
       } else {
           return find4(arr,l, midIndex - 1);
       }
   }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 8, 9, 10, 11, 10000};
        arr = new int[]{1, 2, 3, 4, 6, 7, 8, 9, 10, 11};
        arr = new int[1000 * 1000];

        for (int i = 0; i < 1000 * 1000; i++) {
            if (i == 900000) {
                arr[i] = arr.length + 10;
            } else {
                arr[i] = i + 1;
            }
        }
        // arr = Util.getRandomArrWithoutRepetition(10, 1, 15);
        // Util.print(arr);
        long now = System.currentTimeMillis();
//        System.out.println(find2(arr));
//        Util.duration(now);


        now = System.currentTimeMillis();
        System.out.println(find3(arr));
        Util.duration(now);
//
//
        now = System.currentTimeMillis();
        System.out.println(find4(arr, 0, arr.length - 1));
        Util.duration(now);
    }
}

合并有序数组

合并有序数组:给定两个排序后的数组A和B，其中A的末端有足够的缓冲空间容纳B。编写一个方法，将B合并入A并排序

逆序对个数

逆序对个数:一个数列，如果左边的数大，右边的数小，则称这两个数位一个逆序对。求出一个数列中有多少个逆序对。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
package com.ep.example;

/***
 * @author dep
 * @version 1.0
 */

import org.assertj.core.api.Assertions;
import org.lanqiao.algo.util.Util;

/**
 * 思路：将数组分为左右两个子数组，递归调用归并进行排序
 *      分别排序完成后，使用辅助的合并函数将两个有序的子数组合并成一个整体有序的数组
 * 时间复杂度：均：O(nlgn)，好：O(nlgn)，坏：O(nlgn)
 * 空间复杂度：需要开辟辅助空间，该辅助空间可以重用，大小为N
 * 非原址排序
 * 稳定性：所有排序都是归并，在左的永远在左，在右的永远在右，稳定
 */
public class exercise13_nixu {
    private static int[] helper;

    public static void sort(int[] arr) {
        helper = new int[arr.length];
        sort(arr, 0, arr.length -1);
    }

    /***
     * 分两段进行排序，然后再合并
     * @param A
     * @param p
     * @param r
     */
    private static void sort(int[] A, int p, int r) {
        if(p < r ){
            int mid = p + ((r - p) >> 1); // 中位数
            sort(A, p, mid); // 左侧排序
            sort(A, mid+1, r); // 右侧排序
            /**
             * 合并的过程中只要抓右侧的数据就有逆序对，因为左侧右侧都是排序好的，
             * 只需要抓左侧，逆序对的个数就是左侧剩余的元素
             */
            merge(A,p,mid,r); // 合并
        }
    }
    static int  niXu = 0;

    /**
     * 假设数组的两段分别有序，借助一个辅助数组来缓存原数组，用归并的思路将元素从辅助数组中拷贝回原数组
     * @param A 原数组
     * @param p 低位
     * @param mid 中间位
     * @param r 高位
     */
    private static void merge(int[] A,int p, int mid, int r) {
        // 拷贝到辅助空间相同的位置
        System.arraycopy(A,p,helper,p, r-p +1);
        // 辅助数组的两个指针
        int left = p, right = mid +1;
        // 原始数组的指针
        int current = p;
        while (left <= mid && right <= r) {
            if(helper[left] <= helper[right]) {
                A[current++] = helper[left++];
            } else { // 右侧小
                A[current++] = helper[right++];
                niXu += mid - left + 1;
            }
        }
        while (left <= mid) {
            A[current] = helper[left];
            current++;
            left++;
        }
    }
    public static void main(String[] args) {
        int[] arr = Util.getRandomArr(10, 1, 100);
        Util.print(arr);
        sort(arr);
        Util.print(arr);
        Assertions.assertThat(Util.checkOrdered(arr, true)).isTrue();
        System.out.println("nixu:" + niXu);
    }
}

堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
package com.ep.sort;

/***
 * @author dep
 * @version 1.0
 * @date 2022-11-22 12:01
 */

import org.assertj.core.api.Assertions;
import org.lanqiao.algo.util.Util;

import java.util.Arrays;

/**
 * 思路：首先要知道大顶堆和小顶堆，数组就是一个堆，每个i节点的左右孩子是2i+1和2i+2
 *      有了堆，将其堆化：从n/2-1个元素开始向下修复，将每个节点修复为小（大）顶堆
 *      修复完成后，数组具有小（大）顶堆的性质
 *      按序输出：小顶堆可以对数组逆序排序，每次交换栈顶和末尾元素，对栈顶进行向下修复，这样次小元素又到堆顶了
 *
 * 时间复杂度： 堆化：一半的元素修复，修复是单分支的，所以整体堆化为nlgn/2
 * 排序：n个元素都要取出，因此调整n次，每次调整修复同上是lgn的，整体为nlgn
 * 空间复杂度：不需要开辟辅助空间
 * 原址排序
 * 稳定性：
 */
public class HeapSort {
    // 建初堆
    static void makeMinHeap(int[] A) {
        int n = A.length;
        for (int i = n/2 -1; i>=0; i--) {
            MinHeapFixDown(A, i, n);
        }
    }
    static void MinHeapFixDown(int[] arr, int i, int n) {
        // 找到左右孩子
        int left = 2 * i +1;
        int right = 2 * i +2;
        // 左孩子已经越界， i就是叶子节点
        if (left >= n) {
            return;
        }
        int min = left;
        if (right >= n) {
            min = left;
        } else {
            if (arr[right] < arr[left]) {
                min = right;
            }
        }
        // min指向了左右孩子中较小的那个

        // 如果arr[i]比两个孩子都要小，不用调整
        if(arr[i] < arr[min]) {
            return;
        }
        // 否则，两个孩子中较小的和i交换
        int temp = arr[i];
        arr[i] = arr[min];
        arr[min] = temp;

        // 小的那个孩子发生了变化，要对这个位置进行递归调整
        MinHeapFixDown(arr, min,n);
    }

    static void sort(int[] arr) {
        // 先对A进行堆化
        makeMinHeap(arr);
        for (int x = arr.length-1; x >= 0; x--) {
            // 堆顶,0号元素和最后一个元素对调
            Util.swap(arr, 0, x);
            // 缩小堆的范围，对堆顶元素进行向下调整
            MinHeapFixDown(arr, 0, x);
        }
    }
    public static void main(String[] args) {
        int[] arr = Util.getRandomArr(10, 1, 100);
        System.out.println( "begin..." + Arrays.toString( arr ) );
        sort(arr);
        System.out.println( "final..." + Arrays.toString( arr ) );
        Assertions.assertThat( Util.checkOrdered( arr, false ) ).isTrue();
    }
}

算法
#算法 #算法很美
算法基础
http://example.com/2022/09/21/04.算法/08.算法基础/
作者
Deng ErPu
发布于
2022年9月21日
许可协议